Chapter 8

Density of CMB photons

The cosmic microwave background (CMB) radiation is often called the "leftover radiation from the Big Bang." In other words, it results from a time when radiation and matter were in equilibrium with each other, with radiation being a natural outcome of this situation (we'll see later where the photons come from). Since the radiation is "in equilibrium," the distribution of photons as a function of wavelength is given by the Planck or blackbody spectrum, which has an associated energy density of $\varepsilon = \alpha T^4$. As photons get redshifted as the universe expands, the blackbody spectrum is maintained with its temperature declining as $T \propto a^{-1}$. Today we can precisely measure this energy density, and compare it to the Benchmark estimate for baryonic matter:

These energy densities change over time differently ($\varepsilon_{\gamma} \propto a^{-4}$ and $\varepsilon_{\rm bary} \propto a^{-3}$), but their number densities both change as $\propto a^{-3}$ (photons lose extra energy due to redshift, but the number of photons or baryons does not change over time). Since the energy per CMB photon is $\sim6.3\times10^{-4}~{\rm eV}$ and the energy per baryon (proton or neutron mass) is 939 MeV, the energy densities can be converted to number densities, and the ratio of the two can be thought of as a fundamental parameter of cosmology, which we call $\eta$:

Therefore, there are over a billion photons for every baryon (for each proton or neutron in existence), and this ratio has remained unchanged since a few microseconds after the Big Bang, when quarks were free particles not tied up in hadrons (protons, neutrons, etc.).

Recombination

Early on in the universe, atoms are all ionized (largely protons and electrons and helium nuclei flying around independently). Photons and charged particles readily interact with each other, so photons get deflected often — in other words, they don't travel far before they get scattered. This scattering is dominated by electrons because they appear "larger" to photons (even though they are point particles, as far as we know) than protons do. The effective size of an electron to a photon is called the Thomson cross-section $\sigma_e = 6.65 \times 10^{-29}~{\rm m}^2$ — in other words, if a photon crosses an area of this size centered on an electron, it'll get scattered by the electron.

Given this cross-section, we can say how far a photon will (on average) travel between scatterings, the mean free path $\lambda_{\rm mfp}$, or similarly how much time passes between scatterings (b/c photons travel at speed $c$), or how many scatterings occur per second, the scattering rate $\Gamma$. Imagine a square area with side length $x$; if we make this square 3-dimensional, so it has a depth given by $\ell$, the number of electrons in that box depends on the number density $n_e$: $N_e = n_e x^2 \ell$. For each electron inside the box, project its position onto the surface of the box and draw a circle around it so that it has an area equal to $\sigma_e$. Once the sum of these areas is equal to the area of the box surface, there is a 100% probability that a photon (traveling in the direction of $\ell$, but could have any position relative to the surface). When this occurs, $\ell = \lambda_{\rm mfp}$.

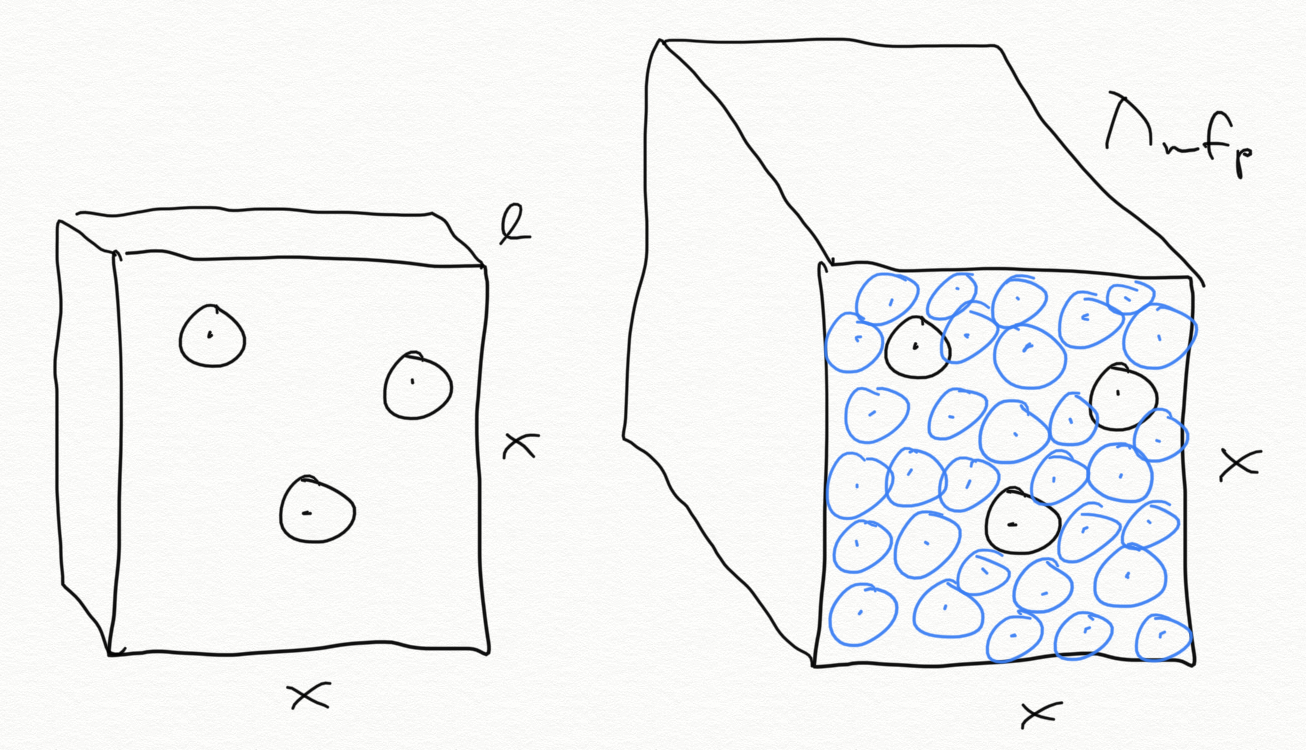
Mathematically, we want the sum of all the cross-sections, given by $N_e \sigma_e$, to equal the area of the box surface, so $x^2 = N_e \sigma_e = n_e x^2 \lambda_{\rm mfp} \sigma_e$, thus

Similarly, the scattering rate is then just $\boxed{\Gamma = \frac{c}{\lambda_{\rm mfp}} = n_e \sigma_e c}$. Assuming the energy per particle remains high enough to prevent electrons and nuclei from forming atoms, photons and electrons will continue to scatter off of each other as long as this scattering rate is higher than the expansion rate of the universe. This isn't an exact equation, but gives you a sense of whether electrons will stay in the box long enough to scatter a photon. So let's say in some amount of time, a photon will get scattered 10 times (so it travels a distance into the box $\ell = 10 \lambda_{\rm mfp}$). If the expansion rate of the universe (given by the Hubble parameter $H$) were such that the scale factor $a$ was growing by a factor of 10 in that same interval of time (so that $\Gamma = H$), the density of electrons in that box would decrease by a factor of $10^3$ as electrons are moving with the expansion of space and being removed from the box. Thus, the mean free path will increase by the same factor, which will then decrease the scattering rate the same amount, so you go from many scatterings to effectively zero scatterings very quickly.

With all this scattering going on (including between protons and electrons), all of these particles will share energy and be in thermal equilibrium with each other, meaning that they share a common temperature. For photons in equilibrium, the number of photons as a function of frequency or wavelength is given by the blackbody distribution. This expression can be integrated over all frequencies to yield the total number density:

For electrons or ions (or any other non-relativistic particle), the number density of particles as a function of their momenta is given by the Maxwell-Boltzmann distribution, and integrating it over all momenta yields the total number density of particle type $x$:

The factor $g_x$ is the statistical weight of the particle ($g=2$ for photons, electrons, protons, and neutrons) and $\mu_x$ is the chemical potential of the particle, which helps determine which direction a reaction runs (and in general $\mu_\gamma = 0$). What we're interested in is the reaction

whereby electrons and protons combine to form a hydrogen atom, with the leftover energy being taken away by a photon, and the symmetric reaction where a photon strikes a neutral atom and ionizes it. The backwards reaction is called recombination (because in many environments in the Galaxy, gas is neutral or is thought to have been neutral originally, and thus the ion and electron are combining again, hence the name). This name is dumb because we're considering protons and electrons combining together for the first time ever. So, I suppose, it is an appropriate technical term for astronomers, who love their terms to be bass-ackwards.

Anyway, because the reaction has an even probability of going either way, the chemical potentials on either side of the equation (for hydrogen and the proton-electron pair) must equal: $\mu_H = \mu_p+\mu_e$. For a given temperature $T$, we can then write down the number density separately for protons, electrons, and hydrogen atoms, but that requires knowing the actual values for the chemical potentials. We can get around this by taking a ratio:

otherwise known as the Saha Equation (important in stellar atmospheres). The new term $Q = (m_p+m_e-m_{\rm H})c^2 = 13.6~{\rm eV}$, or the ionization energy of hydrogen.

For high temperatures, the exponential term will be close to 1 and the other term will be small (due to the $T^{-3/2}$ term), which is what we expect — everything should be ionized. For low temperatures, the function blows up due to the exponential factor, which makes sense because the protons and electrons will form atoms, depleting the number of free protons and electrons.

What we want to find out is at what temperature the transition between these two states occur, or at what temperature recombination happens. If we define the dimensionless ionization fraction $X$ like so:

so that a fully ionized plasma has $X=1$ and a fully neutral gas has $X=0$, we can say recombination happens when $X = 0.5$ (half way from fully ionized to fully neutral).

We can't quite solve for $T$ yet however, because there are 3 densities and $X$ only combines 2 of them into a single variable, so we need another equation. Using the last equality in the equations for $X$ above, we can also use the equation for $n_\gamma$, which is only a function of $T$, to get a unique solution. Unfortunately, this set of equations need to be solved numerically, which yields

The temperature is then $T_{\rm rec} = 3760~{\rm K} = T_0 (1+z_{\rm rec})$, which occurred at a redshift of $\boxed{z_{\rm rec} = 1380}$, or 250,000 years after the Big Bang (to get this time, you need $a(t)$, which is not an analytic function in the Benchmark model). The universe switches over from being radiation-dominated to matter-dominated at $a_{\rm rm} = 2.9 \times 10^{-4}$, or $t_{\rm rm} = 50,000~{\rm yr}$, so recombination happens when the universe is matter-dominated.

Decoupling

While we've found when recombination "happened," by choosing $X = 0.5$, in reality the transition takes some time (around 70,000 years). Now what we want to know is when matter decouples from radiation — in other words, photons are no longer scattering off of electrons often enough for them to exchange energy (read: stay coupled to each other). As mentioned above, this occurs as long as the scattering rate is higher than the universe's expansion rate, or $\Gamma > H$. During recombination, the scattering rate is plummeting because electrons are getting gobbled up into atoms (neutral atoms don't scatter photons).

The function for $n_e(z)$ comes from recognizing that $\varepsilon = \varepsilon_0 a^{-3}$ for baryons, which also holds for their number density since the energy is completely tied up in their mass. $X(z)$ comes into it from the equations for $X$ above, converting $n_e$ into $n_{\rm bary}$ (which just changes with the scale factor or redshift).

The expansion rate comes from the Friedmann equation, which at this time can be approximated for a flat, matter-only universe: $H^2/H_0^2 = \Omega_{\rm m,0} a^{-3} = \Omega_{\rm m,0} (1+z)^3$ so

Setting these equal gets the redshift of decoupling, $z_{\rm dec} = 1120$. BUT, as the number free electrons goes down, the reaction $H+\gamma \rightleftharpoons p+e^-$ is no longer symmetric (i.e., $\mu_H \ne \mu_p+\mu_e$). The correct (and more complicated) calculation yields $\boxed{z_{\rm dec} = 1090}$.

Last Scattering

All these calculations are meant to understand the origin of the CMB as we observe it. Just like with the surface of the Sun, where what we see is the surface defined by the last time a photon scattered off something (thus traveling in a straight line to us). So, to understand the image of the CMB we see, we need to know when those photons last scattered before continuing on to our telescopes.

Statistically, the last time a photon scattered can be calculated by integrating over the scattering rate as a function of time (or redshift). This gives us the optical depth $\tau$; when $\tau = 1$, the average scattering rate is 1 divided by the time integrated over, or that over that time only 1 scattering should have taken place:

This integral isn't hard to write out, then it can be integrated numerically, but the correct calculation is more complicated, and, ultimately, it's good enough to state that the redshift of last scattering is the same as decoupling: $\boxed{z_{\rm ls} \approx z_{\rm dec} \approx 1090}$.

Temperature fluctuations

To use the spatial variations in temperature of the CMB to learn about cosmology, we need to be able to measure how large the fluctuations are. To convert angular sizes $\theta$ to physical sizes $\ell$, all we need is the angular diameter distance $d_A = \ell / \theta \approx d_{\rm hor}(t_0) / z$, where the last part is valid when $z \gg 1$. In the Benchmark Model, $d_{\rm hor}(t_0) \approx 14~{\rm Gpc}$, so the physical size of angles on the CMB is given by

The horizon distance at the time of last scattering ($t_{\rm ls}$) is the largest distance scale over which particles and photons could scatter off each other (and those scatterings are what allow the particles to reach thermal equilibrium). Since the universe is first radiation dominated, then matter dominated, but the cosmological constant remains very weak throughout, so we can use the form for $a(t)$ in a flat universe with only radiation and matter in

The fluctuations are actually caused by sound waves created when overdense regions (in the dark matter distribution) gravitationally attract baryons and photons (which are still coupled, before last scattering). As the gas falls in, it heats up as the density of gas increases, which increases its pressure, which then causes the baryons and photons to bounce back out of the potential well. For some potentially wells, this can happen multiple times: gas falls in —> heats up —> bounces out —> cools down —> repeat. These oscillations happen at the speed of sound, and the hottest spots on the CMB occur on scales when last scattering happened just as the gas reached its maximum compression.

OK, so consider a region where gas has fallen in for the first time and reaches maximum compression when decoupling occurs. The gas would have traveled at the speed of sound (which depends on the equation of state parameter: $c_s = c \sqrt{w}$). For most of cosmic time up to this point, the photons dominate the energy density, so the baryon-photon fluid sound speed is roughly $c_s = c / \sqrt{3}$. Since the horizon distance is the distance light can travel over the age of the universe, this means that the distance the gas would have covered in that same time is $d_s(t_{\rm ls}) \approx d_{\rm hor}(t_{\rm ls}) / \sqrt{3}$. So, we know the physical distance traveled by the gas, the redshift and thus angular diameter distance to this event, and we can measure the angular scale of the fluctuation. In the above equation for the horizon distance, we used the functional form of $a(t)$ assuming the universe was flat, but since we know both $\ell$ and $\theta$, we can directly calculate $d_A$ or equivalently the horizon distance, which will depend on cosmological parameters (particularly the curvature of the universe). As we've seen, negatively curved universes make observed angles smaller, and positively curved ones make them larger. So, the angular scale of the fluctuations constrain all the cosmological parameters that go into $a(t)$, although most of the sensitivity is to the curvature. Fluctuations also provide tight constraints on the value of $\eta$, the baryon to photon ratio, which yield the number given at the top of this page.